2018SummerHZOI讨论

HZOI专题讨论

东南大学 张建东 2018年8月

平衡树

BST

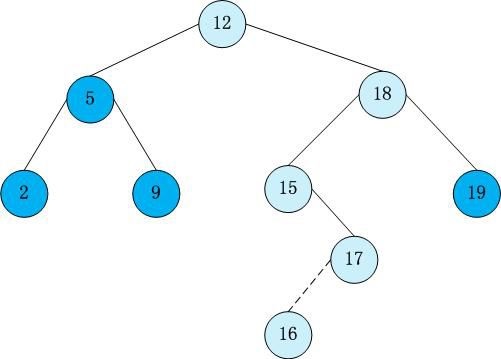
先复习一下二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

插入

向二叉搜索树中插入新元素时，必须先检测这个元素是否在树中已经存在。如果已经存在，则不进行插入，如果元素不存在则将新元素插入到搜索停止的时候，也就是每次插入都是一个叶子节点。

以上图为例，模拟插入6、13、20的过程。

查找

在一棵不为空的二叉搜索树中查找元素时，如果要查找的元素与根节点的值相等，则返回true 或根节点，如果小于根节点的值，则在左子树查找，如果大于根节点的值，在其右子树中查找。否则，返回false或者NULL。

以上图为例，模拟查找9、17、 21的过程。

删除

情况较多，这里不再赘述，具体可以参考

思考

如果一棵树除根节点外的每一棵子树都无左子树或都无右子树，那么上述三种操作的效率如何？

答案：此时树会退化为链，效率由$O(log n)$退化为$O(n)$。

如何解决？ 👇

Treap

treap是一种常用易写的平衡树，单从字母意思来看，treap=tree+heap。

其中，tree就是BST ，heap是堆。所以treap也可以叫树堆。

treap具有以下性质：^1

• Treap是关于key的二叉排序树（也就是规定的排序方式）。
• Treap是关于priority的堆（按照随机出的优先级作为小根/大根堆)。（非二叉堆，因为不是完全二叉树）
• key和priority确定时，treap唯一。

为什么除了权值还要在用一个随机值作为排序方法呢?随机分配的优先级，使数据插入后更不容易退化为链。就像是将其打乱再插入。所以用于平衡二叉树。

根据名字，不难写出如下定义：

定义

struct tNode{
	int s[2],pri,v,size;
    void init(int x,int y){
    	v = x; size = 1; pri = y;
    }
}T[N];

其中s[2]为当前节点的两个儿子,pri表示优先级,是一个随机值，v代表当前结点点权。

更新

void Update(int &i,int val){
    T[i].size = T[L(i)].size + T[R(i)].size + T[i].cnt;//我上面没有写cnt,cnt用于统计重复的点
}

旋转

void Rot(int &y,int f){ //y为根,f是旋转方向
    int x = T[y].s[!f];
    T[y].s[!f] = T[x].s[f];
    T[x].s[f]  = y;
    Update(y);Update(y=x);
}

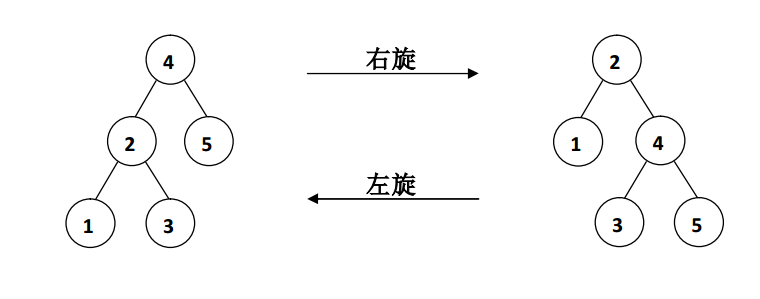
以上图为例，右旋操作就是将root=4的左子树的根节点lson=2的右子树变为root=4的左子树，原来的左子树lson=2变为树根,再将原树根变成现在树根的右子树。左旋同理，所以代码可以仅用f,!f或f^1简写。 套用上面的代码:Rot(4,1);

插入

void Insert(int &i,int val){
    if(!i){
        T[i=++tot].init(val,rand()); //此处rand最好手写，见下文。
        return;
    }
    int f = T[i].v > val;
    Insert(T[i].s[!f],val);
    if(T[T[i].s[!f]].pri > T[i].pri) Rot(i,f);
    else                             Update(i);
}

上述代码可以手画一棵depth<=3的满二叉树模拟一下，较易理解，此处不多解释。

关于rand函数，用过pascal的同学都知道pascal的随机性能较好，noip考场对拍也一般选择用pascal出随机数据。treap是一种高效的平衡树，为了不让c++的内置rand影响性能，尤其当treap被卡常数时，我们可以手写rand:[^3]

inline int rand(){
    static int seed = 2333; //seed为随机数种子，可以修改
    return seed = (int)((((seed ^ 998244353) + 19260817ll) * 19890604ll) % 1000000007);
}

删除

• 先找到要删除的节点的位置. ^1
• 如果这个节点位置上有多个相同的数,则直接cnt–.
• 如果只有一个儿子或者没有儿子,直接将那个儿子接到这个节点下面(或将儿子赋值为0).
• 如果有两个儿子,现将随机值小的那个旋到这个位置,将根旋下去,然后将旋之后的情况转化为前几种情况递归判断.

void Del(int &i,int v){
    if(T[i].v==v){
        if(!L(i)||!R(i)){//如果只有0~1棵子树
            if((!L(i))&&(!R(i))){//如果是0棵子树
                T[i].size = 0;
                i = 0;return;
            }//如果是1棵子树
            if(!T[i].s[0]) i = T[i].s[1];
            else           i = T[i].s[0];
        }
        else{//将优先级较大的旋转上来
            int f = T[L(i)].pri > T[R(i)].pri;
            Rot(i,f);
            Del(T[i].s[f],v);
        }
    }else Del(T[i].s[v>T[i].v],v);
    Update(i);
}

Another solution:^1

void delet(int &x, int val){
    if(!x) return;//防止越界
    if(t[x].val == val){
        if(t[x].cnt > 1){t[x].cnt--, t[x].size--;return;}//有相同的就直接cnt--
        bool d = t[ls].rd > t[rs].rd;
        if(ls == 0 || rs == 0) x = ls+rs;//只有一个儿子就直接把那个儿子放到这个位置
        else rotate(x, d), delet(x, val);//否则将x旋下去,找一个随机值小的替代,直到回到1,2种情况
    }
    else t[x].size--, delet(t[x].ch[t[x].val<val], val);//递归找到要删除的节点.
}

查排名

int ranks(int i,int v){
    if(!i) return 0;
    if(T[i].v >= v) return ranks(L(i),v);
    else            return T[L(i)].size + 1 + ranks(R(i),v);
}

查前驱后继

int prev(int i,int v){
    if(!i) return -inf;
    if(T[i].v < v) return max(T[i].v,prev(R(i),v));
    else           return prev(L(i),v);
}

int succ(int i,int v){
    if(!i) return inf;
    if(T[i].v> v) return min(T[i].v,succ(L(i),v));
    else          return succ(R(i),v);
}

查找第k小数

int Rank(int i,int kth){
    if(T[L(i)].size + 1 == kth) return i;
    else if(T[L(i)].size >=kth) return Rank(L(i),kth);
    else return Rank(R(i),kth - T[L(i)].size - 1);
}

例题讲解

POJ1442 Black Box

• 题意：有一个数列，初始为空，和一个index，初始是0。给出两种操作，第一种是往数列中添加一个数，第二种是将i++，再查询数列中第i小的数是多少。(操作数<=3w)

• 做法： 裸平衡树。

• 代码

  #include<bits/stdc++.h>
  using namespace std;
  const int N = 100100;
  #define L(i) (T[i].s[0])
  #define R(i) (T[i].s[1])
  #define For(i,n) for(int i=1;i<=n;i++)
  #define Rep(i,l,r) for(int i=l;i<=r;i++)
  
  struct treap{
      int size,s[2],v,pri;
      void Sets(int x,int y){
          size = 1;v = x;pri = y;
      }
  }T[N];
  
  int n,m,A[N],size,Lim,now,level = 0;
  int tot,root;
  int read(){
      char ch = getchar(); int num = 0 , q = 1;
      while(ch>'9'||ch<'0'){
          if(ch=='-') q = -1;
          ch = getchar();
      }
      while(ch>='0'&&ch<='9'){
          num = num * 10 + ch - '0';
          ch = getchar();
      }
      return num * q;
  }
  
  void Update(int i){
      T[i].size = T[L(i)].size + T[R(i)].size + 1;
  }
  
  void Rot(int &y,int f){
      int x = T[y].s[!f];
      T[y].s[!f] = T[x].s[f];
      T[x].s[f]  = y;
      Update(y);Update(x);
      y = x;
  }
  
  void Insert(int &i,int val){
      if(!i){
          T[i=++tot].Sets(val,rand());
          return;
      }
      int f = T[i].v > val;
      Insert(T[i].s[!f],val);
      if(T[T[i].s[!f]].pri > T[i].pri) Rot(i,f);
      else                             Update(i);
  }
  
  int Rank(int i,int kth){
      if(T[L(i)].size + 1 == kth) return i;
      else if(T[L(i)].size >=kth) return Rank(L(i),kth);
      else return Rank(R(i),kth - T[L(i)].size - 1);
  }
  
  int main(){
      srand(time(NULL));
      n = read(); m = read();
      For(i,n) A[i] = read();
      For(i,m) {
          Lim = read();
          Rep(i,now+1,Lim) Insert(root,A[i]); now = Lim;
          level++;printf("%d\n",T[Rank(root,level)].v);
      }
      return 0;
  }

POJ2299 Ultra-QuickSort

• 题意：给出长度为$n(n<50000)$的数列,求出该数列的逆序对数。

• 做法：动态插入数字，每次插入数字后得到数字的当前排名，当前总数-当前排名即为该数产生的逆序对数。

• 代码：

  #include<bits/stdc++.h>
  using namespace std;
  const int N = 500010;
  #define Ch1 (T[i].s[0])
  #define Ch2 (T[i].s[1])
  #define For(i,n) for(int i=1;i<=n;i++)
  #define Rep(i,l,r) for(int i=l;i<=r;i++)
  
  void read(int &v){
      char ch=getchar();
      int num=0;
      while(ch>'9'||ch<'0') ch=getchar();
      while(ch>='0'&&ch<='9'){
          num=num*10+ch-'0';
          ch=getchar();
      }
      v=num;
  }
  
  struct treap{
      int v,size,pri;
      int s[2];
      void Sets(int x,int y){v=x;pri=y;size=1;}
  }T[N];
  
  int n,x,cnt,root;
  long long ans;
  
  void Update(int i){
      T[i].size=T[Ch1].size+T[Ch2].size+1;
  }
  
  void Rot(int &y,int f){
      int x=T[y].s[!f];
      T[y].s[!f]=T[x].s[f];
      T[x].s[f]=y;
      Update(y);Update(x);
      y=x;
  }
  
  void Insert(int &i,int x){
      if(!i){
          T[i=++cnt].Sets(x,rand());
          T[i].s[0]=T[i].s[1]=0;
          return;
      }
      int f=T[i].v>x;
      Insert(T[i].s[!f],x);
      if(T[T[i].s[!f]].pri>T[i].pri) Rot(i,f);
      else                           Update(i);    
  }
  
  int find(int i,int x){
      if(T[i].v==x) return T[Ch1].size+1;
      if(T[i].v<x) return T[Ch1].size+1+find(Ch2,x);
      if(T[i].v>x) return find(Ch1,x);
  }
  
  int main(){
      while(read(n),n){
          ans=0;
          cnt=root=0;
          For(i,n){
              read(x);
              Insert(root,x);     
              ans+=i-(find(root,x));         
          }
          cout<<ans<<endl;
      }
      return 0;
  }

BZOJ3196(TYVJ1730)二逼平衡树

• 题意：

  您需要写一种数据结构（可参考题目标题），来维护一个有序数列，其中需要提供以下操作：

  1.查询k在区间内的排名

  2.查询区间内排名为k的值

  3.修改某一位值上的数值

  4.查询k在区间内的前驱(前驱定义为小于x，且最大的数)

  5.查询k在区间内的后继(后继定义为大于x，且最小的数)

• 做法？ Code

练习题

1. POJ3481 Double Queue
2. POJ2352 Stars

Splay

可以先看一看Treap与Splay等其他平衡树的比较[^2]。

基本概念不再赘述，只介绍一下Splay的三种旋转。

旋转

• Zig Step[^4]

  

  此处旋转同Treap。

• Zig-Zag Step

  

  当p不是根节点，且x和p同为左孩子或右孩子时进行Zig-Zig操作。

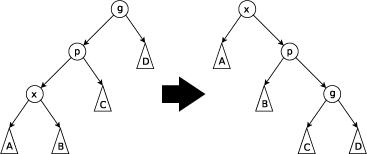
  当x和p同为左孩子时，依次将p和x右旋；

  当x和p同为右孩子时，依次将p和x左旋。

• Zig-Zig Step

  

  当p不是根节点，且x和p不同为左孩子或右孩子时，进行Zig-Zag操作。

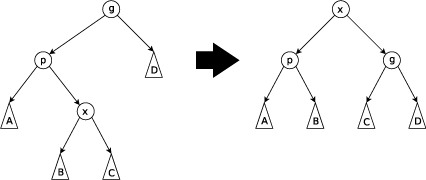
  当p为左孩子，x为右孩子时，将x左旋后再右旋。

  当p为右孩子，x为左孩子时，将x右旋后再左旋。

可以发现，所有情况都可以归结为上面三种旋转。

通过深度为3的二叉树模拟，可以总结出下述写法:[^5]

#define fa(i) (T[i].p)
#define Loc(i) (T[fa(i)].s[1]==i)
#define For(i,n) for(int i=1;i<=n;i++)
#define Rep(i,l,r) for(int i=l;i<=r;i++)
#define Sets(P,i,tp) {T[P].s[tp]=i; fa(i)=P;} 
void Rot(int i){
    int x = i , y = fa(x) , z = fa(y);
    int lx = Loc(x) , ly = Loc(y) , lz = Loc(z);
    Sets(y,T[x].s[!lx],lx);
    Sets(z,i,ly);
    Sets(i,y,!lx);
    T[y].cnt[lx] = T[x].cnt[!lx];
    T[x].cnt[!lx] = T[y].cnt[0] + T[y].cnt[1] + T[y].num;
}

void Splay(int i,int goal){
    for(;fa(i)!=goal;){
        if(fa(fa(i))!=goal) Rot(fa(i));
        Rot(i);
    }
    if(!goal) root = i;
} 

思想

Splay Tree可以方便的解决一些区间问题，根据不同形状二叉树先序遍历结果不变的特性，可以将区间按顺序建二叉查找树。

每次自下而上的一套splay都可以将x移动到根节点的位置，利用这个特性，可以方便的利用Lazy的思想进行区间操作。

对于每个节点记录size，代表子树中节点的数目，这样就可以很方便地查找区间中的第k小或第k大元素。

对于一段要处理的区间[x, y]，首先splay x-1到root，再splay y+1到root的右孩子，这时root的右孩子的左孩子对应子树就是整个区间。

这样，大部分区间问题都可以很方便的解决，操作同样也适用于一个或多个条目的添加或删除，和区间的移动。

再推荐一篇文章: Splay Tree

例题讲解

郁闷的出纳员

题意：

做法：我们已经学过了treap,那么这题采用treap是否可行？

答案当然是可行的^_^, 觉得不可行的面壁思过去。而且这题也没有用splay的必要。splay只在处理区间问题时有独特优势，其余情况下因为其编程复杂度不低，常数较大，故大部分oier优先采用treap。本题是个裸的splay，对整体打lazy标记即可，但要注意一个坑点是如果初始工资就已经低于工资下届，这个员工是不用考虑Insert的。

代码：

#include<bits/stdc++.h>
using namespace std;
#define fa(i) (T[i].p)
#define Loc(i) (T[fa(i)].s[1]==i)
#define For(i,n) for(int i=1;i<=n;i++)
#define Rep(i,l,r) for(int i=l;i<=r;i++)
#define Sets(P,i,tp) {T[P].s[tp]=i; fa(i)=P;} 
struct tnode{
    int p,s[2],v,num,cnt[2];
}T[100100];

int n,Lim,mark,num,Left,root,tot;

void Rot(int i){
    int x = i , y = fa(x) , z = fa(y);
    int lx = Loc(x) , ly = Loc(y) , lz = Loc(z);
    Sets(y,T[x].s[!lx],lx);
    Sets(z,i,ly);
    Sets(i,y,!lx);
    T[y].cnt[lx] = T[x].cnt[!lx];
    T[x].cnt[!lx] = T[y].cnt[0] + T[y].cnt[1] + T[y].num;
}

void Splay(int i,int goal){
    for(;fa(i)!=goal;){
        if(fa(fa(i))!=goal) Rot(fa(i));
        Rot(i);
    }
    if(!goal) root = i;
} 

void Insert(int V,int i){
    if(!i){
        root=++tot;
        T[tot].v = V;T[tot].p = 0;T[tot].num = 1;
        return;
    }
    if(T[i].v==V) T[i].num++;    
    else{
        T[i].cnt[V>T[i].v]++;
        if(!T[i].s[V>T[i].v]){
            T[i].s[V>T[i].v]=++tot;
            T[tot].v = V;T[tot].p = i;T[tot].num = 1;
            Splay(tot,0);
        }
        else Insert(V,T[i].s[V>T[i].v]);
    }
}

int rank(int kth,int i){
    if(!i) return i;
    if(T[i].cnt[1]<kth&&T[i].cnt[1] + T[i].num >= kth) return i;
    else if(kth<T[i].cnt[1]+T[i].num)  return rank(kth,T[i].s[1]);
    else                               return rank(kth-T[i].cnt[1]-T[i].num,T[i].s[0]);
}

int Prev(int i){
    int Next = T[i].s[0];
    while(T[Next].s[1]) Next = T[Next].s[1];
    return Next;
}

void Delete(int i){
    Left+=T[i].num;
    Splay(i,0);
    if(T[i].s[0]){
        Splay(Prev(i),i);
        Sets(T[i].s[0],T[i].s[1],1);
        fa(T[i].s[0]) = 0;
        root = T[i].s[0];
    }else{
        if(T[i].s[1]){root=T[i].s[1];fa(T[i].s[1]) = 0;}
        else          root = 0;
    }
    T[i].cnt[0] = T[i].cnt[1] = T[i].num = T[i].s[0] = T[i].s[1] = 0;
}

int main(){
    scanf("%d%d",&n,&Lim);
    For(i,n){char op;
        scanf("\n%c %d",&op,&num);
        T[0].v = -mark - 1;
        if(op=='I') 
          if(num>=Lim)  Insert(num-mark,root);
        if(op=='A')     mark+=num;
        if(op=='F')     printf("%d\n",T[rank(num,root)].v+mark);
        if(op=='S'){
            mark-=num;
            Rep(j,1,tot)
              if(T[j].num>0&&T[j].v+mark<Lim) Delete(j);
        }
    }
    printf("%d\n",Left);
    return 0;
}

tyvj1729文艺平衡树

(这个OJ貌似已经改版了，现在的名字叫Joy OI, 你们可以自己搜一下)

题意：

您需要写一种数据结构（可参考题目标题），来维护一个有序数列，其中需要提供以下操作： 翻转一个区间，例如原有序序列是5 4 3 2 1，翻转区间是[2,4]的话，结果是5 2 3 4 1

做法：我们已经学过了treap, 那么这题采用treap是否可行呢？

Splay对区间的操作、lazy标记。 我刚学的时候一直没懂这个splay的操作，对区间[a,b]的操作，首先把a-1splay到树根，然后再把b+1旋转到树根的右子树。这个很好理解，但是我一开始写的是直接T[i].s[v>T[i].v]访问，一直不对，一直很纳闷，后来模拟了一下，才发现真正有效的是splay的排名，lazy标记下传后，左右子树被交换，但默认的排名未变。即第i号元素不一定就是i。

代码：

#include <set>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
#define fa(i) (T[i].p)
#define Ch1 (T[i].s[0])
#define Ch2 (T[i].s[1])
#define Loc(i) (T[fa(i)].s[1]==i)
#define Sets(a,b,c) {T[a].s[c] = b;fa(b) = a;}
#define For(i,n) for(int i=1;i<=n;i++)
#define Rep(i,l,r) for(int i=l;i<=r;i++)

struct tnode{
    int s[2],size,p,V,flag;
}T[N];

int ttot,l,r,n,m,root;

void Pushdown(int i){
    if(T[i].flag){
        if(Ch1) T[Ch1].flag ^= 1;
        if(Ch2) T[Ch2].flag ^= 1;
        swap(Ch1,Ch2);
        T[i].flag = 0;
    }
}

void Build(int l,int r,int p,int &i){
    if(l>r) return;
    int m = ( l + r ) >> 1;
    T[i=++ttot].V = m;
    T[i].p = p; T[i].size = 1;
    Build(l,m-1,i,Ch1);
    Build(m+1,r,i,Ch2);
    T[i].size = T[Ch1].size + T[Ch2].size + 1;
}

void Rot(int x){
    int y = fa(x) , z = fa(y);
    Pushdown(y);Pushdown(x);
    int lx = Loc(x) , ly = Loc(y);
    Sets(y,T[x].s[!lx],lx);
    Sets(z,x,ly);
    Sets(x,y,!lx);
    T[y].size = T[T[y].s[0]].size + T[T[y].s[1]].size + 1;
}

void Splay(int i,int goal){
    while(fa(i)!=goal){
        if(fa(fa(i))!=goal) Rot(fa(i));
        Rot(i);
    }
    T[i].size = T[Ch1].size + T[Ch2].size + 1;
    if(!goal) root = i;
}

int Find(int i,int rank){
    Pushdown(i);
    if(T[Ch1].size + 1 == rank) return i;
    else if(T[Ch1].size>= rank) return Find(Ch1,rank);
    else                        return Find(Ch2,rank-T[Ch1].size-1);
}

void OUT(int i,int rank){
    if(!i) return;
    Pushdown(i);
    OUT(Ch1,rank);
    rank+=T[Ch1].size+1;
    if((rank!=1)&&(rank!=n+2)){
        if(rank==n+1) printf("%d\n",T[i].V);
        else          printf("%d ",T[i].V);
    }
    OUT(Ch2,rank);
}


int main(){
    scanf("%d%d",&n,&m);
    Build(0,n+1,0,root);
    For(i,m){
        scanf("%d%d",&l,&r);
        Splay(Find(root,l),0);
        Splay(Find(root,r+2),root);
        T[T[T[root].s[1]].s[0]].flag ^= 1;
    }
    OUT(root,0);
    return 0;
}

练习题

1. HNOI2004宠物收养所
2. HNOI2002营业额统计
3. ZJOI2007报表统计
4. BZOJ1251序列终结者
5. SCOI2013多项式运算
6. AHOI2006文本编辑器
7. POJ3580 SuperMemo（必做)

treap和splay的练习题和例题都是以前我做过的题目,虽然年代久远但是比较经典。

另外，平衡树的实用性其实不高，已经逐渐淡出算法竞赛的舞台，通过例题和练习题所标出的年份也不难发现这一点。

平衡树淡出除了过于模板、实用性不高以外，还有另外一个原因，就是C++的STL里封装了RBT(红黑树)，大家可以多多学习STL的内容。

STL

STL网上教程、文章较多，此处不多赘述。

给出如下建议：掌握>熟悉>了解

名称	建议
vector、map、set	掌握
upper_bound、lower_bound	掌握
list、stack、deque	了解
multimap、multiset	熟悉
queue、priority_queue	掌握

熟练使用迭代器(iterator)，掌握upper_bound，lower_bound等常用方法，熟悉unique等方法。

LCA

LCA(Least Common Ancestors)问题是指给定一棵树T和两个节点u和v，找出u和v的离根节点最远的公共祖先。

以下图为例，求(3,12) , (14,4) , (7,9)的LCA。

Tarjan算法

​ LCA的Tarjan算法的时间复杂度为$O(n+q)$，是一种离线算法，要用到并查集。

　　Tarjan算法基于dfs，在dfs的过程中，对于每个节点位置的询问做出相应的回答。

　　dfs的过程中，当一棵子树被搜索完成之后，就把他和他的父亲合并成同一集合；在搜索当前子树节点的询问时，如果该询问的另一个节点已经被访问过，那么该编号的询问是被标记了的，于是直接输出当前状态下，另一个节点所在的并查集的祖先；如果另一个节点还没有被访问过，那么就做下标记，继续dfs。

例题讲解

POJ 1330 Nearest Common Ancestors

题意：给出一棵树，($n<=10000$)，询问两点间的LCA。

直接上代码，结合代码理解一下流程。

#include<bits/stdc++.h>
using namespace std;
const int N = 10010;
#define rep(i,n) for(int i=1;i<=n;i++)
#define GetRoot rep(i,n)if(!indeg[i]){root = i;break;}
int u,v,n,head[N],indeg[N],root,ans;
int fa[N];bool vis[N];
struct edge{
    static int es;
    int t,next;
    void add(int s,int t){
        this->t = t; next=head[s];head[s]=es++;
    }
    static void clear(){
        es=0;
        memset(vis,0,sizeof(vis));
        memset(indeg,0,sizeof(indeg));
        memset(head,-1,sizeof(head));
    }
}e[N];
int edge::es = 0;


int find(int i){
    return (fa[i]==i)?(i):(fa[i]=find(fa[i]));
}

void Tarjan(int rt){
    if(ans) return;
    for(int i=head[rt];i+1;i=e[i].next){
        Tarjan(e[i].t);
        fa[find(e[i].t)]=rt;
    }
    vis[rt]=true;
    if(rt==u && vis[v]) ans = find(v);
    if(rt==v && vis[u]) ans = find(u);
}

int main(){
    int _;
    scanf("%d",&_);
    while(_--){
        ans=0;edge::clear();
        scanf("%d",&n);fa[n]=n;
        rep(i,n-1){
            fa[i]=i;int x,y;
            scanf("%d%d",&x,&y);
            indeg[y]++;
            e[edge::es].add(x,y);
        }
        scanf("%d%d",&u,&v);
        GetRoot;
        Tarjan(root);
        cout<<ans<<endl;
    }
    return 0;
}

HDU2586 How far away ?

题意：给出一棵树，($n<=40000$)，每条边均有权值，询问两点间的最短路径。

思路：树上两点间的最短路径往往要想到LCA，noip近些年也有涉及。

不难发现树中两点间最短路径即是$d(u)+d(v)-2d(LCA)$,其中$d(x)$是$x$到根节点的距离。

另外注意，本题中给出的虽是无向图，但是可以按有向图处理出一个根节点，方便操作。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 40010;
typedef pair<int,int> pii;
#define mp make_pair
#define fx first
#define fy second
#define GetRoot(rt) rep(i,n)if(!indeg[i]){rt = i;break;}
#define START int _;scanf("%d",&_);while(_--)
#define rep(i,n) for(int i=1;i<=n;i++)
int dis[N],head[N],n,m,ans[N],fa[N],indeg[N];
bool vis[N];
vector<pii> q[N];
struct edge{
    static int es;
    int t,next,v;
    static void clear(){
        es=0;
        rep(i,n) {
            fa[i]=i;
            q[i].clear();
        }
        memset(head,-1,sizeof(head));
        memset(vis,0,sizeof(vis));
        memset(ans,0,sizeof(ans));
        memset(indeg,0,sizeof(indeg));
    }
    void add(int x,int y,int w){
        v=w;t=y;next=head[x];head[x]=es++;
    }
}e[N<<1];
int edge::es = 0;


int find(int k){
    return fa[k]==k?k:fa[k]=find(fa[k]);
}

int dfs(int u){
    for(int i=head[u];i+1;i=e[i].next){
        int v=e[i].t; 
        dis[v]=dis[u]+e[i].v;
        dfs(v);
    }
}

void Tarjan(int u){
    for(int i=head[u];i+1;i=e[i].next){
        int v=e[i].t;
        if(vis[v]) continue;
        Tarjan(v);
        fa[find(v)]=u;
    }
    vis[u]=true;
    for(int i=0;i<q[u].size();i++)
        if(vis[q[u][i].fx] && !ans[q[u][i].fy]){
            ans[q[u][i].fy] = dis[q[u][i].fx] + dis[u] - 2*dis[find(q[u][i].fx)];
        }
}

int main(){
    START{int rt,x,y,w;
        scanf("%d%d",&n,&m);
        edge::clear();
        rep(i,n-1){
            scanf("%d%d%d",&x,&y,&w);
            e[edge::es].add(x,y,w);
            indeg[y]++;
        }
        rep(i,m){
            scanf("%d%d",&x,&y);
            q[x].push_back(mp(y,i));
            q[y].push_back(mp(x,i));
        }
        GetRoot(rt);
        dis[rt]=0;dfs(rt);
        Tarjan(rt);
        rep(i,m) printf("%d\n",ans[i]);
    }
    return 0;
}

倍增

倍增算法处理LCA问题非常容易理解，也不难写，在近些年的noip、NOI、冬令营都有出现，建议熟练掌握。

在处理(a,b)的LCA问题时，不难想到的一种思路是将(a,b)调至同一深度，然后(a’,b’)同时上/下调，使其到达同一个顶点，这个顶点就是(a,b)的LCA。倍增算法就是基于这种思路的优化，具体优化在调整上。

考虑$fa(i,j)$表示节点$i$,向上跳$2^j$个单位后到达的顶点，那么显然$fa(i,j)=fa(fa(i,j-1),j-1)$

（不显然？手动算算或者仔细想想$fa(i,j-1)$向上需要跳多少步才能到$fa(i,j)$? )

按照类似的思路我们还可以维护$dis(i,j), max(i,j)$等。

例题讲解

NOIP2013T3 货车运输

题意：一个可能有重边的图，给出若干个询问，求点对间路径中的最小边的最大值。

对于 30%的数据，$0 < n < 1,000，0 < m < 10,000，0 < q < 1,000$；

对于 60%的数据，$0 < n < 1,000，0 < m < 50,000，0 < q < 1,000$；

对于 100%的数据，$0 < n < 10,000，0 < m < 50,000，0 < q < 30,000，0 ≤ z ≤ 100,000$。

做法：其实只需对图跑一个最大生成树，暴力处理询问就可以拿60分。对于100%的询问，直接倍增LCA。

代码:

#include<bits/stdc++.h>
using namespace std;
const int N = 50010*2;
const int M = 50010;
#define logn 16
#define For(i,n) for(int i=1;i<=n;i++)
#define Rep(i,l,r) for(int i=l;i<=r;i++)
#define Down(i,r,l) for(int i=r;i>=l;i--)

struct edge{
    int s,t,next,w;
}E[M*2],TE[M];

int q,n,m,Es,s,t,w;
int f[N],fa[N][logn+20],deep[N],Min[N][logn+20];
int head[N];
bool vis[N];

void makelist(int s,int t,int w){
    E[Es].s = s;E[Es].t = t; E[Es].w = w; 
    E[Es].next = head[s];head[s] = Es++;
}

bool cmp(edge A,edge B){
    return A.w > B.w;
}

int find(int i){
    return (f[i]==i)?(i):(find(f[i]));
}

void init(){
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);    
    For(i,n) f[i] = i;
    For(i,m){
        scanf("%d%d%d",&s,&t,&w);
        TE[i].s = s;TE[i].t = t;TE[i].w = w;
    }
    sort(TE+1,TE+m+1,cmp);
    For(i,m){
        int fx = find(TE[i].s) , fy = find(TE[i].t);
        if(fx!=fy) {
            f[fx] = fy;
            makelist(TE[i].s,TE[i].t,TE[i].w);
            makelist(TE[i].t,TE[i].s,TE[i].w);
        }
    }
}

void DFS(int i){            
    vis[i] = true;
    for(int p=head[i];p!=-1;p=E[p].next)
        if(!vis[E[p].t]){
            int v = E[p].t;fa[v][0] = i;
            deep[v] = deep[i] + 1;
            Min[v][0] = E[p].w; 
            For(j,logn){
                fa[v][j] = fa[fa[v][j-1]][j-1];
                Min[v][j] = min(Min[v][j-1],Min[fa[v][j-1]][j-1]);
            }
            DFS(v);
        }
}

int LCA(int u,int v){
    int ans = 2147483647;if(deep[u] < deep[v]) swap(u,v);
    int d = deep[u] - deep[v];
    Rep(i,0,logn)
        if((1<<i)&d) {ans = min(ans,Min[u][i]);u = fa[u][i];}
    if(u==v) return ans;
    Down(i,logn,0)
      if(fa[u][i]!=fa[v][i]){
          ans = min(min(Min[u][i],Min[v][i]),ans);
          u = fa[u][i];v = fa[v][i];
      }
    if(u!=v){
        ans = min(ans,min(Min[u][0],Min[v][0]));
        u = fa[u][0];
    }
    return ans;
}

int main(){
    init();
    For(i,n)
      if(!deep[i]){deep[i] = 1;DFS(i);}
    scanf("%d",&q);
    For(i,q){
        scanf("%d%d",&s,&t);
        if(find(s)!=find(t)) printf("%d\n",-1);
        else                 printf("%d\n",LCA(s,t));
    }
    return 0;
}

NOIP2015 T6 运输计划

题意：给出$n(<=300000)$个节点的树，和$m(<=300000)$个询问点对间最短距离。要求选择一条边，使该边权值为0后，求出m个询问的最大值最小。

样例：

思考：

我参加了这一年的考试，没记错的话暴力+奇技淫巧应该能拿到60分？现在针对100%的数据来看。

分析完题目之后发现其实就是“最大值最小”类问题，第一反应是二分。将所有询问处理出来后（怎么处理？），每次二分答案$ans$，对超出答案的询问处理，怎么处理呢?

显然，对超出答案的所有询问的路径求交，交出的路径中求出最大的边$max$，以$ans-max$为二分依据即可。

路径求交，采用差分（也有叫树上前缀和）：在树中将所有路径起、始权值+1，LCA权值-2，从所有叶节点往上累加，最终权值为路径数的点到其父亲的边为所求边。

时间复杂度：$O(mlogn+(m+n)logL) $

RMQ、树链剖分

展开讲很费时间，还是推荐几篇文章：

1. LCA转RMQ
2. RMQ与LCA(From TopCoder Algorithm Tutorials)
3. 树链剖分求LCA
4. 树剖求LCA
5. 树剖法

练习题

1. POJ1470Closest Common Ancestors
2. POJ1986Distance Queries
3. NOIp2012 疫情控制

DP优化

DP优化有很多种类型，常见的有下面四种。[^6][^7]

数据结构优化

线段树、树状数组

这类问题的状态方程一般都不是很难，往往分析之后都能得出常见的如LIS（最长上升子序列）等模型。

NOIP2013T5 花匠

其实是个很简单的dp，设$f[i][j]$表示前i位其中第$i$位状态为$j$的方案数，$j=0,1$分别代表低和高，那么

$f[i][j]=max{f[k][j\text{^}1]}+1$,其中$h[i],h[k]$需要满足相应的条件。

对$j$分类讨论，如当$j=0$时,$f[i][0]=max{f[j][1]} + 1 , h[j]>h[i]$，那么只需对$h$建树，在$h[i]\text{~}\infty$找最大值即可。

单调栈、单调队列

这类问题的核心是单调，考虑$f[i]=min{f[j]+w[i]}$，如果$w[i]$单调增，则只需用递减的单调队列维护$f[j]$即可。

Vijos1243生产商品[^8]

题意：有$n$个任务，$m$个机器，每个机器完成每个任务都有特定的时间，任务必须依次完成，且一个机器只能连续完成$l$个任务，每次更换机器需要时间$k$，求完成所有任务的最短时间。($n<=100000,m<=5$)

分析：首先预处理$s[i][j]$为第$i$个机器完成前$j$个任务所需要的时间,$f[i][j]$为完成前$i$个任务且第$i$个任务为$j$号机器完成的时间，那么有如下的转移方程

$f[i][j] = min{f[k][p] +s[j][i]-s[j][k]} , i-l<=k<i$,显然，这样做的时间复杂度是$O(nm^2l)$,但是将式子变形成$f[i][j] = min{f[k][p] -s[j][k]} +s[j][i] , i-l<=k<i$, 就不难发现了单调性，此时可以用单调队列维护，复杂度变成了$O(nm^2)$。

单调栈其实和单调队列类似，都是分析单调性。具体可以做做练习题6。

斜率优化

对于$f[i]=min{f[j] + (x[i]-x[j])^2}$形转移方程，将其展开后得到$f[i]=min{f[j]+x[j]^2+x[i]^2-2 x[i]x[j]}$,显然，如果没有最后的交叉项，可以用单调队列维护。现在有了这个交叉项，我们可以考虑斜率优化。

HDU3507Print Article

该题的转移方程其实就是$f[i]=min{f[j]+x[j]^2+x[i]^2-2 x[i]x[j]+m}$,和上式基本相同。考虑$k<j<i$, 且用$j$更新比用$k$更新好。则有$f[j]+(x[i]-x[j])^2+m < f[k]+(x[i]-x[k])^2 +m$,移项化简得 $\frac{(f[j]+x[j]^2)-(f[k]+x[k]^2)}{x[j]-x[k]}<2 x[i]$，此时令$Y[j]=(f[j])+x[j]^2) , Y[k]=(f[k]+x[k]^2) , X[i]=x[i] , F[i]=2 x[i]$, 则上式变为$\frac{Y[j]-Y[k]}{X[j]-X[k]}<F[i]$,该式就是最经典的斜率式，换言之，只要满足上式，选$j$一定比选$k$优。其实化简得核心就是利用单调队列维护斜率。

四边形优化

推荐文章：四边形不等式优化讲解（详解）

矩阵加速

大家对斐波那契数列一定都非常熟悉，$f(n)=f(n-1)+f(n-2)$，显然对于$n<=1e8$是可以轻松处理的，但是如果当n非常大，比如$n>1000000000$，如何处理呢？

引入矩阵：$$M = \begin{bmatrix} 0& 1 \newline 1 & 1 \end{bmatrix} ，f_n=\begin{bmatrix} f(n-1)\newline f(n)\end{bmatrix} ,f_{n+1} = \begin{bmatrix}f(n) \newline f(n+1)\end{bmatrix}$$,那么显然$f_{n+1}=M \cdot f_n$，换言之$f_{n+1} = M^n \cdot f_1$。我们知道普通数字的$n$次幂是可以通过快速幂求出的，矩阵也有类似的性质。所以我们可以采用矩阵快速幂的方法优化dp的转移方程。

关于矩阵快速幂，可以做经典例题POJ3233 Matrix Power Series

例题讲解

HDU5950 Recursive sequence

题面：

这题是2016 ACM-ICPC 沈阳站的铜牌题，题目意思其实就是求$an=2a_{n-2}+a_{n-1}$.其中$n>=3, a_1 = a ,a_2 =b$给出。

由于$n<2^{31}$，故考虑矩阵加速,构造矩阵$$M=\begin{bmatrix} 0&1 \newline 2&1 \end{bmatrix}$$即可。

其他

如状压dp、数位dp、树型dp等是特殊形式的dp，也建议大家找找例题练习掌握。

练习题

1. 【Easy】矩阵加速

2. 【Medium】HNOI2008GT考试(结合kmp)

3. 【Medium】 SCOI2009迷路

4. 【Easy】POJ3017Cut the Sequence]

5. 【Hard】BZOJ1791:Island

6. 【Medium】 HNOI2008玩具装箱toy

7. 【合集】斜率优化 入门经典

8. bzoj1096 [ZJOI2007]仓库建设

   bzoj1597 [USACP2008 Mar]土地购买

   bzoj1911 [Apio2010]特别行动队

   bzoj3156 防御准备

   bzoj3675[Apio2014] 序列分割

   bzoj3437 小P的牧场

   bzoj4518 [SDOI2016] 征途

由于本人水平有限，如有错误敬请批评指正。 祝同学们在接下来的NOIp、冬令营、省选中取得好成绩！

[^2]: Treap与SBT, RBT, Splay比较
[^3]: treap学习总结
[^4]: Splay 学习笔记
[^5]: Splay伸展树
[^6]: DP优化小结
[^7]: 常见DP优化类型总结
[^8]: 单调队列优化dp例题