用简短的python代码实现光线追踪(一)
介绍光线追踪是图形学中非常常用的一种成像方式,并在不同的领域(如游戏、动画、电影)得到了广泛的应用。而类似本文这样的关于光线追踪的入门文章也数不胜数,但鲜有用python实现的文章。本文将以python为主要实现语言,编写一个Ray Tracing的渲染器。
(至于为何使用python, 单纯是因为python简单易写,可调的包丰富)
基本知识按照惯例,在说光线追踪之前,务必要提到光栅化(Rasterization)。所谓光栅化,就是将几何模型经过一系列变换(MVP),最终转换为像素呈现在显示设备上的过程。即对于一个object, 扫描其
Reference
CS4620: Introduction to Computer Graphics (cornell.edu)
GAMES101:现代计算机图形学入门 – 计算机图形学与混合现实研讨会 (games-cn.org)
Fundamentals of Computer Graphics, Fourth Edition
Ray Tracing in One Weekend Series
怎样可以清除GitHub中不想要的commit,并使他不占空间(强迫症)
有三种方式可以消除commit,但是都无法彻底删除相应文件空间: git reset, git revert, git rebase -i
关于删除空间,可以先查看哪些文件占的空间较大:
1git rev-list --objects --all | grep "$(git verify-pack -v .git/objects/pack/*.idx | sort -k 3 -n | tail -5 | awk '{print$1}')"
然后删除对应的文件
123git filter-branch --force --index-filter \ 'git rm --cached --ignore-unmatch ___bigfile___' \ --prune-empty --tag-name-filter cat -- --all
再彻底从commit中抹掉该文件的记录:
123git for-each-ref --format='delete %(refname)' refs ...
Pandas中SettingWithCopyWarning是如何产生并解决的?
两个主要原因
SettingWithCopyWarning通常在用户使用副本时产生,具体会发生在以下两种情况:
链式赋值(Chained assignment) 如df[a:b][c:d] = x,该操作包含两次链式操作,第一次会生产新的dataframe,第二次的赋值刷在该新的df上进行。 解决方案是使用loc,即df.loc[a:b,c:d] = x
蔽链(Hidden chaining) 如下面的代码,df2是由df经过get操作得来的,前者可能是后者的副本,也有可能不是。当修改df2的时候,有可能修改了df,所以也会出现Warning.
12df2 = df.loc[df.a==df.b]df2.loc[c,d] = x
解决方案是明确说明df2是df的副本,即:
1df2 = df.loc[df.a==df.b].copy()
如果你很清楚以上原因,可以直接关闭警告: pd.set_option('mode.chained_assignment', None)
ReferenceSettingwithCopyWarning: How to Fix ...
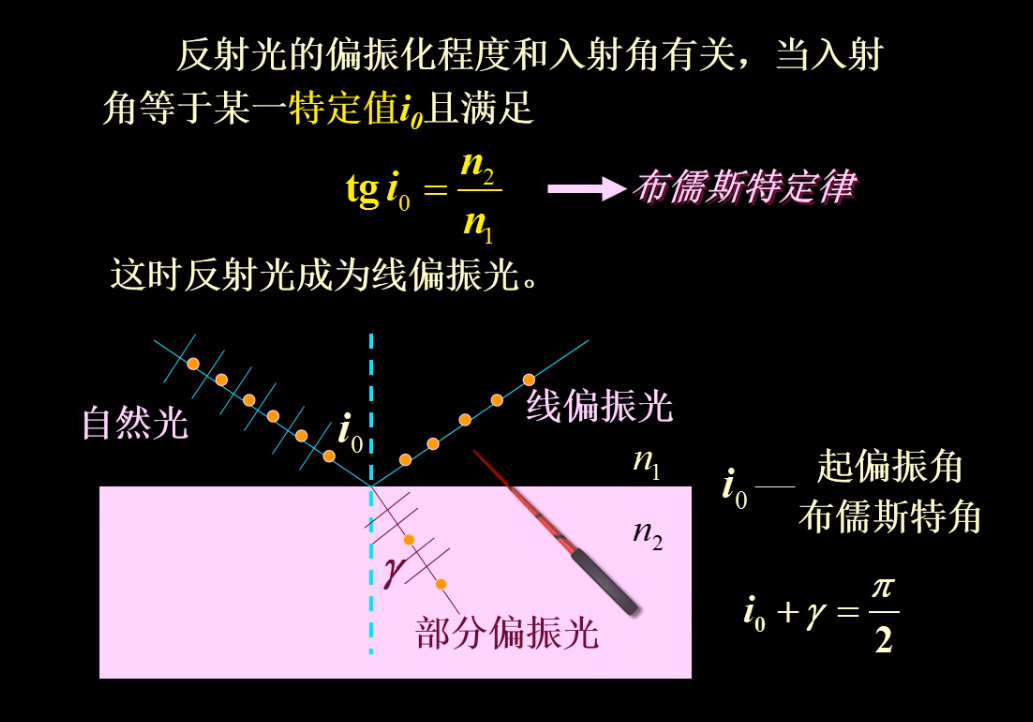
大学物理下期末复习
Author : Jerome
参考公式显示不全、错误的直接看pdf:大物下册考点、公式合集(zjd整理)
清华物理题库(对应下册部分)
B1模拟卷
B1模拟卷答案
辅导讲座ppt
振动
加速度$a$和位移大小$x$成正比, 且方向相反的运动称为简谐振动, $a=\frac{d^2x}{dt^2} = -w^2x$
该微分方程的解为$x = A\cos(wt+\varphi)$,求导得$v = \frac{dx}{dt}=-wA\sin(wt+\varphi),a=\frac{d^2x}{dt^2}=-w^2A\cos(wt+\varphi)$
弹簧振子$w=\sqrt\frac{k}{m}, T=2\pi\sqrt\frac{k}{m}, v = \frac{1}{2\pi}\sqrt\frac{k}{m}$, 其中$T$与$v$只与振动系统本身得物理性质有关, 这种只与振动系统本身固有属性所决定的周期和频率称为固有周期和固有频率.
限定$|\Delta\varphi|\ ...
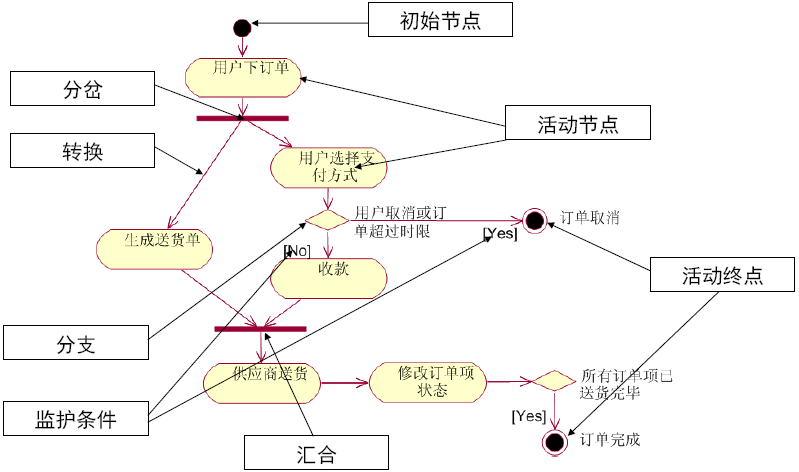
面向对象技术与UML期末复习
Object Oriented Technology and UML ReviewAuthor : Jerome
Exam Date : 11.8 Thu. 6-7 Lesson
Classroom : J1-211
Overview and IntroductionKey points in UML Review
UML means Unified Modeling Language , 统一建模语言 in Chinese.
Important goal of software engineering : solving the software crisis.
Software complexity is inherent. Reduce and control the complexity ofsoftware.
The basic method of controllingsoftware complexity: Divide, Abstract, Modularization, Information hiding.
Software Pr ...
2018SummerHZOI讨论
HZOI专题讨论东南大学 张建东
2018年8月
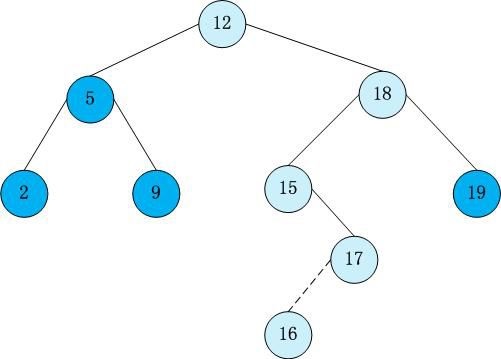
平衡树BST先复习一下二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
插入向二叉搜索树中插入新元素时,必须先检测这个元素是否在树中已经存在。如果已经存在,则不进行插入,如果元素不存在则将新元素插入到搜索停止的时候,也就是每次插入都是一个叶子节点。
以上图为例,模拟插入6、13、20的过程。
查找在一棵不为空的二叉搜索树中查找元素时,如果要查找的元素与根节点的值相等,则返回true 或根节点,如果小于根节点的值,则在左子树查找,如果大于根节点的值,在其右子树中查找。否则,返回false或者NULL。
以上图为例,模拟查找9、17、 21的过程。
删除情况较多,这里不再赘述,具体可以参考
思考如果一棵树除根节点外的每一棵子树都无左子树或都无右子树,那么上述三种操作的效率如何?
答案:此时树 ...
高等数学A(下)期末复习
高数试题考点简要分析多元函数微分学
全微分 $dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy$
例题:12-13-3 二(1)
填空题考法:给出全微分求参数
例题:12-13-3 一(6)
复合函数求微分
隐函数求微分
例题:P31 例4.9(三种方法)
方程组确定隐函数: P33 例4.10
空间曲线的切线与法平面
切向量:$\alpha = \lbrace x’(t_0),y’(t_0),z’(t_0)\rbrace$
切线:$\frac{x-x_0}{x’(t_0)}=\frac{y-y_0}{y’(t_0)}=\frac{z-z_0}{z’(t_0)}$
法平面:$x’(t_0)(x-x_0)+y’(t_0)(y-y_0)+z’(t_0)(z-z_0)=0$
例题:P43 例6.3
空间曲面的切平面与法线
法向量:$n=\lbrace F_x(x_0,y_0,z_0),F_y(x_0,y_0,z_0),F_z ...
离散数学期末复习
考试结构
10道选择题(含多选,但答案不超过两个)20分3道证明题来自于集合论和代数结构(重难点)
数理逻辑
# 命题逻辑的基本概念
命题与联结词命题(Proposition)
概念:具有唯一真值的陈述句
唯一性:或真或假但不能两者都是的
命题所用符号:常用小写26个英文字母
经典例子
$x=3$ ×
我现在说假话 × (悖论)
请不要吸烟! ×(祈使句)
这朵花真美丽啊! (感叹句)
悖论:既不能为真,也不能为假的陈述句称作 __悖论__。
注
命题是陈述句,陈述句不一定是命题命题有唯一真值,但真值可能受范围、时空、环境、判断标准、认识程度限制,一时无法确定
命题分类
简单命题:不能被分解成更简单的命题
复合命题:简单命题+联结词(Connective)
联结词(Connective)
否定联结词(Negation Connective)
符号¬,读作“非”,“否定”
定义:命题 p
p的否定式:复合命题“p的否定”(“非p”)
符号:$\neg$ p (符号$\neg$称作否定联结词)
$\neg$ p为真当且仅当p为假
例子
今天没 ...
大一下学期面向对象程序设计(1)期末复习
期末复习总览占比分布期末 70%
作业 20%
考勤 10%
笔试阅读程序 4题各5分
填空 2题各10分 5空
上机 3*20分
考试要点构造函数、析构函数拷贝构造函数什么时候使用? 传值,返回值
例子(共调用3+2次) :
add(cls x,cls y){
return x+y;
}
add(x,y)
常成员函数Composition函数初始化先对成员对象初始化,构造函数初始化列表
static操作符重载必须重载为全局函数
虚函数纯虚函数后加 = 0
栈展开对象释放
分章复习Chapter 9 类(1)条件编译`#ifndef FILENAME_H`
`#define FILENAME_H`
`#endif`
Sizeof只包括数据成员的大小
VC为了确保结构的大小为结构的字节边界数(即该结构中占用最大空间的类型所占用的字节数)的倍数,所以在为最后一个成员变量申请空间后,还会根据需要自动填充空缺的字节。
比较以下例子
class test1{
char c;
...